THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING (MRI)

THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING
(MRI
By : Sumarsono


History
Felix Bloch and Edward Purcell, both of whom were awarded the Nobel Prize in 1952, discovered the magnetic resonance phenomenon independently in 1946. In the period between 1950 and 1970, NMR was developed and used for chemical and physical molecular analysis.
In 1971 Raymond Damadian showed that the nuclear magnetic relaxation times of tissues and tumors differed, thus motivating scientists to consider magnetic resonance for the detection of disease. Magnetic resonance imaging was first demonstrated on small test tube samples that same year by Paul Lauterbur. He used a back projection technique similar to that used in CT. In 1975 Richard Ernst proposed magnetic resonance imaging using phase and frequency encoding, and the Fourier Transform This technique is the basis of current MRI techniques. A few years later, in 1977, Raymond Damadian demonstrated MRI called field-focusing nuclear magnetic resonance. In this same year, Peter Mansfield developed the echo-planar imaging (EPI) technique. Edelstein and coworkers demonstrated imaging of the body using Ernst's technique in 1980. A single image could be acquired in approximately five minutes by this technique. By 1986, the imaging time was reduced to about five seconds, without sacrificing too much image quality. The same year people were developing the NMR microscope, which allowed approximately 10 mm resolution on approximately one cm samples. In 1987 echo-planar imaging was used to perform real-time movie imaging of a single cardiac cycle. In this same year Charles Dumoulin was perfecting magnetic resonance angiography (MRA), which allowed imaging of flowing blood without the use of contrast agents.



In 1991, Richard Ernst was rewarded for his achievements in pulsed Fourier Transform NMR and MRI with the Nobel Prize in Chemistry. In 1992 functional MRI (fMRI) was developed. This technique allows the mapping of the function of the various regions of the human brain. Five years earlier many clinicians thought echo-planar imaging's primary applications was to be in real-time cardiac imaging. The development of fMRI opened up a new application for EPI in mapping the regions of the brain responsible for thought and motor control. In 1994, researchers at the State University of New York at Stony Brook and Princeton University demonstrated the imaging of hyperpolarized 129Xe gas for respiration studies. In 2003, Paul C. Lauterbur of the University of Illinois and Sir Peter Mansfield of the University of Nottingham were awarded the Nobel Prize in Medicine for their discoveries concerning magnetic resonance imaging. MRI is clearly a young, but growing science.
The Basic Physics
The human body is primarily fat and water. Fat and water have many hydrogen atoms which make the human body approximately 63% hydrogen atoms. Hydrogen nuclei have an NMR signal. For these reasons magnetic resonance imaging primarily images the NMR signal from the hydrogen nuclei. Each voxel of an image of the human body contains one or more tissues. Within each cell there are water molecules. Each water molecule has one oxygen and two hydrogen atoms. One hydrogen atom contain one proton (single proton).

THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING
(MRI)
Spin
The proton possesses a property called spin which: it can be thought of as a small magnetic field, and will cause the nucleus to produce an NMR signal.

Spin is a fundamental property of nature like electrical charge or mass. Spin comes in multiples of 1/2 and can be + or -. Protons, electrons, and neutrons possess spin. Individual unpaired electrons, protons, and neutrons each possesses a spin of 1/2. In the deuterium atom ( 2H ), with one unpaired electron, one unpaired proton, and one unpaired neutron, the total electronic spin = 1/2 and the total nuclear spin = 1. Two or more particles with spins having opposite signs can pair up to eliminate the observable manifestations of spin. An example is helium. In nuclear magnetic resonance, it is unpaired nuclear spins that are of importance. Spin of proton like a magnetic moment vector, causing the proton to behave like a tiny magnet with a north (N) and south pole (S).
A collection of 1H nuclei (spinning protons) in the absence of an externally applied magnetic field. The magnetic moments have random orientations.When the proton is placed in an external magnetic field B0, the spin vector of the particle aligns itself with the external field, one of two orientations with respect to B0 (denoted parallel and anti-parallel). Protons aligned in the parallel orientation are said to be in a low energy state. Protons in the anti-parallel orientation are said to be in a high-energy state.

The energy differential between the high and low energy states is proportional to the strength of the externally applied magnetic field B0. Also related to the strength of B0 is the number of spins in the low energy state. The higher the B0, the greater the number of spins aligned in the low-energy state. The number of spins in the low energy state in excess of the number in the high-energy state is referred to as the spin excess. The magnetic moments of these excess spins add to form the net magnetization and thus the tissue placed in the magnetic field becomes magnetized. The net magnetization is also represented as a vector quantity. As previously mentioned, a larger B0 will produce a greater spin excess. Therefore, a larger B0 will produce a larger net magnetization vector.
Larmor’s Formula
The spin vektor do not line up precisely with external magnetic field but at an angle to the field, and they rotate about the direction of the magnetic field similar to the wobbling motion of a spinning top. This wobbling motion is called precession and occurs at a specific frequency (rate) for a given atom’s nucleus in a magnetic field of a specific strenght.
The Larmor equation expresses the relationship between the strength of a magnetic field, B0, and the precessional frequency, ωo, of an individual spin. From The Larmor Equation that the precessional frequency is equal to the strength of the external static magnetic field (B0) multiplied by the gyromagnetic ratio (γ). Increasing B0 will increase the precessional frequency and conversely, decreasing B0 will decrease the precessional frequency. This is analogous to a spinning top. It will precess due to the force of gravity. If the gravity were to be decreased (as it is on the moon), then the top would precess slower.
Wo = γ BO
The proportionality constant to the left of B0 is known as the gyromagnetic ratio of the nucleus. The precessional frequency, ωo, is also known as the Larmor frequency. For a hydrogen nucleus, the gyromagnetic ratio is 4257 Hz/Gauss. Thus at 1.5 Tesla (15,000 Gauss), ωo = 63.855 Megahertz.



Fourier Transformation
To understand how an image is constructed in MRI it is first instructive to take a look at Fourier Transformation (FT). FT permits signal to be decomposed into a sum of sine waves each of different frequency, phases and amplitudes.

S(t) = a0 + a1sin(1t + 1) + a2sin(2t + 2) + ...
The FT of the signal in the time domain can be represented in the equivalent frequency domain by a series of peaks of various amplitudes. In MRI the signal is spatially encoded by changes of phase/frequency which is then unravelled by performing a 2D FT to identify pixel intensities across the image.

MRI Signal Production
Hydrogen exists in many molecules in the body. Water (consisting of two hydrogen atoms and one oxygen) comprises up to 70% of body weight. Hydrogen is also present in fat and most other tissues in the body. The varying molecular structures and the amount of hydrogen in various tissues effect how the protons behave in the external field. As an example, because of the total amount of hydrogen in water, it has one of the strongest net magnetization vectors relative to other tissues. Other structures and tissues within the body have less hydrogen concentration and become magnetized to a lesser extent. In other words, their net magnetization is less intense.
The amount of mobile hydrogen protons that a given tissue possesses, relative to water (specifically CSF), is referred to as its spin density (proton density). This is the basis with which we begin to produce images using Magnetic Resonance. The hydrogen nucleus contains one proton and possesses a significant magnetic moment. In addition, hydrogen is very abundant in the human body. By placing the patient in a large external magnetic field, will magnetize the tissue (hydrogen), preparing it for the MR imaging process.
A radio wave is actually an oscillating electromagnetic field. It is oriented perpendicular to the main magnetic field (B0). If a pulse of RF energy apply into the tissue at the Larmor frequency, the individual spins begin to precess in phase, as will the net magnetization vector. As the RF pulse continues, some of the spins in the lower energy state absorb energy from the RF field and make a transition into the higher energy state. This has the effect of tipping the net magnetization toward the transverse plane.


The angle through which M has rotated away from the z-axis is known as the flip angle. The strength and duration of B1 determine the amount of energy available to achieve spin transitions between parallel and anti-parallel states. Thus, the flip angle is proportional to the strength and duration of B1. Pulses of 90 degrees is applied to produce a 90-degree flip of the net magnetization. A pulse of 180 degrees rotates M into a position directly opposite to B0, with greater numbers of spins adopting anti-parallel (rather than parallel) states. If the B1 field is applied indefinitely, M tilts away from the z-axis, through the x-y plane towards the negative z direction, and finally back towards the x-y plane and z-axis (where the process begins again).
As the magnetization (now referred to as transverse magnetization, or Mxy) precesses through the receiver coil, a current or signal is induced in the coil. The principle behind this signal induction is Faradays Law of Induction. This states that if a magnetic field is moved through a conductor, a current will be produced in the conductor. the increasing the size of the magnetic field, or the speed with which it moves, will increase the size of the signal (current) induced in the conductor .
In order to detect the signal produced in the receiver coil, the transmitter must be turned off. When the RF pulse is discontinued, the signal in the coil begins at a given amplitude (determined by the amount of magnetization precesssing in the transverse plane and the precessional frequency) and fades rapidly away. This initial signal is referred to as the Free Induction Decay or FID

The return of M to its equilibrium state (the direction of the z-axis) is known as relaxation. The signal fades as the individual spins contributing to the net magnetization loose their phase coherence, making the vector sum equal to zero. Flipped nuclei start off all spinning together known as T2 relaxation, but quickly become incoherent (out of phase). The FID decays at a rate given by disturbances in magnetic field (magnetic susceptibility) increase the rate of spin coherence T2 relaxation known as T2* (T2-star). At the same time, but independently, some of the spins that had moved into the higher energy state give off their energy to their lattice and return to the lower energy state, causing the net magnetization to regrow along the z axis. This regrowth occurs at a rate given by the tissue relaxation parameter known as T1. The total NMR signal is a combination of the total number of nuclei (proton density), reduced by the T1, T2, and T2* relaxation components.
Magnet inhomogeneity
It is virtually impossible to construct an NMR magnet with perfectly uniform magnetic field strength, B0. Much additional hardware is supplied with NMR machines to assist in normalising the B0 field. However, it is inevitable that an NMR sample will experience different B0's across its body so that nuclei comprising the sample (that exhibit spin) will have different precessional frequencies (according to the Larmor equation). Immediately following a 90 degree pulse, a sample will have Mx-y coherent. However, as time goes on, phase differences at various points across the sample will occur due to nuclei precessing at different frequencies. These phase differences will increase with time and the vector addition of these phases will reduce Mx-y with time.
T1 relaxation
Following termination of an RF pulse, nuclei will dissipate their excess energy as heat to the surrounding environment (or lattice) and revert to their equilibrium position. Realignment of the nuclei along B0, through a process known as recovery, leads to a gradual increase in the longitudinal magnetisation. The time taken for a nucleus to relax back to its equilibrium state depends on the rate that excess energy is dissipated to the lattice. Let M-0-long be the amount of magnetisation parallel with B0 before an RF pulse is applied. Let M-long be the z component of M at time t, following a 90 degree pulse at time t = 0. It can be shown that the process of equilibrium restoration is described by the equation.



where T1 is the time taken for approximately 63% of the longitudinal magnetisation to be restored following a 90 degree pulse.


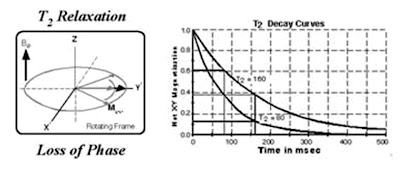
T2 relaxation
While nuclei dissipate their excess energy to the lattice following an RF pulse, the magnetic moments interact with each other causing a decrease in transverse magnetisation. This effect is similar to that produced by magnet inhomogeneity, but on a smaller scale. The decrease in transverse magnetisation (which does not involve the emission of energy) is called decay. The rate of decay is described by a time constant, T2*, that is the time it takes for the transverse magnetisation to decay to 37% of its original magnitude. T2* characterises dephasing due to both B0 inhomogeneity and transverse relaxation. Let M-0-trans be the amount of transverse magnetisation (Mx-y) immediately following an RF pulse. Let M-trans be the amount of transverse magnetisation at time t, following a 90 degree pulse at time t = 0. It can be shown that
Mtrans = Motrans.e-t/T2*

In order to obtain signal with a T2 dependence rather than a T2* dependence, a pulse sequence known as the spin-echo has been devised which reduces the effect of B0 inhomogeneity on Mx-y. A pulse sequence is an appropriate combination of one or more RF pulses and gradients (see next section) with intervening periods of recovery. A pulse sequence consists of several components, of which the main ones are the repetition time (TR), the echo time (TE), flip angle, the number of excitations (NEX), bandwidth and acquisition matrix.



The signal intensity
The signal intensity on the MR image is determined by four basic parameters: 1) proton density, 2) T1 relaxation time, 3) T2 relaxation time, and 4) flow. Proton density is the concentration of protons in the tissue in the form of water and macromolecules (proteins, fat, etc). The contrast on the MR image can be manipulated by changing the pulse sequence parameters. A pulse sequence sets the specific number, strength, and timing of the RF and gradient pulses.
The two most important parameters are the repetition time (TR) and the echo time (TE). The TR is the time between consecutive 90 degree RF pulse. The TE is the time between the initial 90 degree RF pulse and the echo. The most common pulse sequences are the T1- weighted and T2-weighted spin-echo sequences. The T1-weighted sequence uses a short TR and short TE (TR < 1000msec, TE < 30msec). The T2-weighted sequence uses a long TR and long TE (TR > 2000msec, TE > 80msec). The T2-weighted sequence can be employed as a dual echo sequence. The first or shorter echo (TE < 30msec) is proton density (PD) weighted or a mixture of T1 and T2. This image is very helpful for evaluating periventricular pathology, such as multiple sclerosis, because the hyperintense plaques are contrasted against the lower signal CSF. More recently, the FLAIR (Fluid Attenuated Inversion Recovery) sequence has replaced the PD image. FLAIR images are T2-weighted with the CSF signal suppressed.


One of the great advantages of MRI is its excellent soft-tissue contrast which can be widely manipulated. In a typical image acquisition the basic unit of each sequence is repeated hundreds of times over. By altering the echo time (TE) or repetition time (TR), i.e. the time between successive 90° pulses, the signal contrast can be altered or weighted. For example if a long TE is used, inherent differences in T2 times of tissues will become apparent. Tissues with a long T2 (e.g. water) will take longer to decay and their signal will be greater (or appear brighter in the image) than the signal from tissue with a short T2 (fat). In a similar manner TR governs T1 contrast. Tissue with a long TR (water) will take a long time to recover back to the equilibrium magnetisation value, so therefore a short TR interval will make this tissue appear dark compared to tissue with a short T1 (fat). When TE and TR are chosen to minimise both these weightings, the signal contrast is only derived from the number or density of spins in a given tissue. This image is said to be 'proton-density weighted'. To summarise:1). T2-weighting requires long TE, long TR 2).T1-weighting requires short TE, short TR 3). PD-weighting requires short TE, long TR
Spatial Localisation
The actual location within the sample from which the RF signal was emitted is determined by superimposing magnetic field gradients on the magnet generating the otherwise homogeneous external magnetic field B0. For example, a magnetic field gradient can be superimposed by placing two coils of wire (wound in opposite directions) around the B0 field with longitudinal axis orientated in the z direction and then by passing direct current through the coils. The magnetic field from the coil pair adds to the B0 field, with the result that one end of the magnet has a higher field strength than the other known as magnetic gradient. According to the Larmor equation, the magnetic field gradient causes identical nuclei to precess at different Larmor frequencies. The frequency deviation is proportional to the distance of the nuclei from the centre of the gradient coil and the current flowing through the coil.


Slice Selection

Frequency Encoding
Three magnetic field gradients, placed orthogonally to one another inside the bore of the magnet, are required to encode information in three dimensions. With a slice selected and excited as described in the previous paragraph, current is switched to one of the two remaining gradient coils (referred to as the frequency encoding gradient). This has the effect of spatially encoding the excited slice along one axis, so that columns of spins perpendicular to the axis precess at slightly different Larmor frequencies. For a homogeneous sample, the intensity of the signal at each frequency is proportional to the number of protons in the corresponding column.
The frequency encoding gradient is turned on just before the receiver is gated on and is left on while the signal is sampled or read out. For this reason the frequency encoding gradient is also known as the readout gradient. The resulting FID is a graph of signal (formed from the interference pattern of the different frequencies) induced in the receiver verses time. If the FID is subjected to Fourier transform, a conventional spectrum in which signal amplitude is plotted as a function of frequency can be obtained. Thus, a graph of signal verses frequency is obtained which corresponds to a series of lines or views representing columns of spins in the slice.
Phase Encoding
Suppose a slice through a homogeneous sample has been selected and excited as described in Slice Selection section, and then frequency encoded according to the previous section. After a short time, the phase of the spins at one end of the gradient leads those at the other end because they are precessing faster. If the frequency encoding gradient is switched off, spins precess (once more) at the same angular velocity but with a retained phase difference. This phenomenon is known as phase memory.
A phase encoding gradient is applied orthogonally to the other two gradients after slice selection and excitation, but before frequency encoding. The phase encoding gradient does not change the frequency of the received signal because it is not on during signal acquisition. It serves as a phase memory, remembering relative phase throughout the slice.
To construct a 256 x 256 pixels image a pulse sequence is repeated 256 times with only the phase encoding gradient changing. The change occurs in a stepwise fashion, with field strength decreasing until it reaches zero, then increasing in the opposite direction until it reaches its original amplitude. At the end of the scan, 256 lines (one for each phase encoding step) comprising 256 samples of frequency are produced. A Fourier transformation allows phase information to be extracted so that a pixel (x, y) in the slice can be assigned the intensity of signal which has the correct phase and frequency corresponding to the appropriate volume element. The signal intensity is then converted to a grey scale to form an image.

MRI Sequences
MRI signal intensity depends on many parameters, including proton density, T1 and T2 relaxation times. Different pathologies can be selected by the proper choice of pulse sequence parameters. Repetition time (TR) is the time between two consecutive RF pulses measured in milliseconds. For a given type of nucleus in a given environment, TR determines the amount of T1 relaxation. The longer the TR, the more the longitudinal magnetisation is recovered. Tissues with short T1 have greater signal intensity than tissues with a longer T1 at a given TR. A long TR allows more magnetisation to recover and thus reduces differences in the T1 contribution in the image contrast. Echo time (TE) is the time from the application of an RF pulse to the measurement of the MR signal. TE determines how much decay of the transverse magnetisation is allowed to occur before the signal is read. It therefore controls the amount of T2 relaxation. The application of RF pulses at different TRs and the receiving of signals at different TEs produces variation in contrast in MR images. Next some common MRI sequences are described.
Spin Echo Pulse Sequence
The spin echo (SE) sequence is the most commonly used pulse sequence in clinical imaging. The sequence comprises two radiofrequency pulses - the 90 degree pulse that creates the detectable magnetisation and the 180 degree pulse that refocuses it at TE. The selection of TE and TR determines resulting image contrast. In T1-weighted images, tissues that have short T1 relaxation times (such as fat) present as bright signal. Tissues with long T1 relaxation times (such as cysts, cerebrospinal fluid and edema) show as dark signal. In T2-weighted images, tissues that have long T2 relaxation times (such as fluids) appear bright.
In cerebral tissue, differences in T1 relaxation times between white and grey matter permit the differentiation of these tissues on heavily T1-weighted images. Proton density-weighted images also allow distinction of white and grey matter, with tissue signal intensities mirroring those obtained on T2-weighted images. In general, T1-weighted images provide excellent anatomic detail, while T2-weighted images are often superior for detecting pathology.
Gradient Recalled Echo Pulse Sequences
Gradient recalled echo (GRE) sequences, which are significantly faster than SE sequences, differ from SE sequences in that there is no 180 degree refocusing RF pulse. In addition, the single RF pulse in a GRE sequence is usually switched on for less time than the 90 degree pulse used in SE sequences. The scan time can be reduced by using a shorter TR, but this is at the expense of the signal to noise ratio (SNR) which drops due to magnetic susceptibility between tissues. At the interface of bone and tissue or air and tissue, there is an apparent loss of signal that is heightened as TE is increased. Therefore it is usually inappropriate to acquire T2-weighted images with the use of GRE sequences. Nevertheless, GRE sequences are widely used for obtaining T1-weighted images for a large number of slices or a volume of tissue in order to keep scanning times to a minimum. GRE sequences are often used to acquire T1-weighted 3D volume data that can be reformatted to display image sections in any plane. However, the reformatted data will not have the same in-plane resolution as the original images unless the voxel dimensions are the same in all three dimensions.
Paramagnetic Contrast Agents
MRI contrast agents are primarily paramagnetic agents designed to enhance the T1 and T2 relaxation times of adjacent hydrogen nuclei. Some agents are classified as T1 active or T2 active. They produce complex effects that vary depending on the RF pulsing sequence. For example, T1 shortening increases the RF signal intensity but T2 shortening decreases it. In many instances paramagnetic contras agents permit the visualization of lesion with shorter TR, thus decreasing scan time.
Paramagnetic contrast agents have been developed for oral, intravenous, and inhalation administration, and although this is an active research area in MRI, at the present time the IV agents have predominated. Gadolinium+3 (Gd+3), which has seven unpaired electrons, has the strongest relaxation rate properties and has proven effective in demonstrating various types of lesions. However, it is extremely toxic and is administered in a complex with DTPA (diethylenetriaminepentaacetic acid) (Gd-DTPA) to ensure detoxifification.
MRI Artefact
The term artefact refers to the occurrence of undesired image distortions, which can lead to misinterpretation of MRI data. The theoretical limit of the precision of measurements obtained from medical images is determined by the point spread function of the imaging device (Rossmann (1969) and Robson et al. (1997)). However, in practice, the limit is determined by the physiological movements of a living subject (e.g. respiration, heartbeat, twitching or tremor). The finite thickness of the slice of tissue imaged may also represent a constraint. If the signals arising from different tissue compartments cannot be separated within each voxel, then an artefact known as partial voluming is produced. This uncertainty in the exact contents of any voxel is an inherent property of the discretised image and would even exist if the contrast between tissues were infinite. Furthermore, chemical shift and susceptibility artefacts (Schenck (1996)), magnetic field and radio frequency non-uniformity, and Field of View and slice thickness calibration inaccuracies can all compromise the accuracy with which quantitative information can be obtained for a structure of interest in the living human body. A detailed analysis of all these effects is, however, beyond the scope of this article.
Gibbs Ringing or Truncation Artefact
This arises due to the finitie nature of sampling. According to Fourier theory, any repetitive waveform can be decomposed into an infinite sum of sinusoids with a particualr amplitude, phase and frequency. In practice, a waveform (e.g. MRI signal) can only be sampled or detected over a given time period and therefore the signal will be under-represented. The artefact is prominent at the interface between high and low signal boundaries and results in a 'ringing' or a number of discrete lines adjacent to the high signal edge.
Phase-wrap or 'Aliasing'
Aliasing can occur in either the phase or frequency direction but is mainly a concern in the phase direction. It is a consequence of Nyquist theory: the sampling rate has to be at least twice that of the highest frequency expected. The effect occurs whenever there is an object or patient anatomy outside the selected field-of-view but within the sensitive volume of the coil. In the frequency direction, this is avoided by increasing the sampling and use of high pass filters. By swapping the direction of phase/frequency encoding or using larger or rectangular fields-of-view the effect can be avoided.
Motion Artefacts (Ghosting)
Ghosting describes discrete or diffuse signal throughout both the object and the background. It can occur due to instabilites within the system (e.g. the gradients) but a common cause is patient motion. When movement occurs the effect is mainly seen in the phase direction. This is because of the discrepancy between the time taken to encode the image in each direction. Frequency encoding, done in one go at the time of echo collection, takes a few ms whereas phase encoding requires hundreds of repetitions of the sequence, taking minutes. Motion causes anatomy to appear in a different part of the scanner such that the phase differences are no longer consistent. Periodic motion e.g. respiratory or cardiac motion can be 'gated' to the acquisiton so that the phase encoding is performed at the 'same' part of the cycle. This extends imaging time as the scanner 'waits' for the appropriate signal but is effective in combating these artefacts. Modern scanners are now so fast that 'breathold' scans are replacing respiratoy compensation. Non-periodic motion e.g. coughing, cannot easily be remedied and patient co-operation remains the best method of reducing these artefacts. In this simple experiment a test object is moved gently during the scan. The effect is dramatic and due to the fourier transform nature of MRI, even this small displacment has produced artefacts throughout the image (the image is shown twice with different 'window' settings to enable the full extent of the artefact to be seen).
Chemical Shift
This artefact arises due to the inherent differences in the resonant frequency of the two main components of an MR image: fat and water. It is only seen in the frequency direction. At 1.5 Tesla there is approximately 220 Hz difference in the fat-water resonance frequency. If this frequency range has not been accommodated in the frequency encoding (governed by the receiver bandwidth and matrix size) then adjacent fat and water in the object will artificially appear in separate pixels in the final image. This leads to a characterisitic artefact of a high signal band (where the signal has 'built up') and an opposite dark band (signal void).
Susceptibility
The susceptibility of a material is the tendancy for it to become magnetised when placed in a magnetic field. Materials with large differences in susceptibility create local disturbances in the magnetic field resulting in non-linear changes of resonant frequency, which in turn creates image distortion and signal changes. The problem is severe in the case of ferromagnetic materials but can also occur at air-tissue boundaries. This example was acquired in a patient who had permanent dental work. It did not create any problems for the patient but the huge differences in susceptibility caused major distortions and signal void in the final image.
• Other Artefacts
An RF or zipper artefact is caused by a breakdown in the integrety of the RF-shielding in the scan room. Interference from an RF source causes a line or band in the image, the position and width of which is determined by the frequencies in the source. A Criss-cross or Herringbone artefact occurs when there is an error in data reconstruction.

Hardware
An MR system consists of the following components: 1) a large magnet to generate the magnetic field, 2) shim coils to make the magnetic field as homogeneous as possible, 3) a radiofrequency (RF) coil to transmit a radio signal into the body part being imaged, 4) a receiver coil to detect the returning radio signals, 5) gradient coils to provide spatial localization of the signals, and 6) a computer to reconstruct the radio signals into the final image. Each component contributes for making the examination faster and easier.
Magnet
Thera are different types of magnet used for diagnostic and research imaging. Permanent magnet has a field strength limited to 0.064 Tesla – 0.3 Tesla. While resistive magnet is ranging from 0.1 – 0.4 Tesla. Super conductive magnet almost unlimited. It can be low as 0.15 T and can go up to 7 T or higher. Cryogens and refrigeration are required for superconductive magnet to keep the system cool to maintain its strength. The stronger the magnet the higher the signal to noise ratio (SNR). Higher gradient system which is measured as mT/m per axes helps to decreased repetition time (TR) and echo imaging time. Shorter TRs and TEs normally reduced the scanning time down to subsecond imaging. With gradient development it is now possible to pursue real time MR scanning.
Radio Frequency (RF) coils
The body part to be examined determines the shape of the antenna coil to be used for imaging. Most coils are round or oval-shaped. And the body part to be examined is inserted into the coil’s open center. Some coils, rather than encircling the body part, are placed directly on the patien over the area of interest. These “ surface coils” are best for thin body parts, such as the limbs, or superficial portions of a larger body structure, such as the orbit within the head or the spine within the torso. Another form of surface coils is the endocavitary coil, in which the imaging coils is designed to fit within a body cavity, such as rectum. This enables a surface coil to be placed close to some internal organs which may be distant from surface coils applied to the exterior body. Endocavitary coils also may be used to image the wall of the cavity itself.
Gradients
The principle role of the gradient coils are to produce linear chnages in magnetic field in each of the x,y and z directions. By combining gradients in pairs of directions, oblique imaging can be performed. Gradient specifications are stated in terms of a slew rate which is equal to the maximum achievable amplitude divided by the rise time. Typical modern slew rates are 150 T/m-s. The gradient coils areshielded in a similar manner to the main windings. This is to reduce eddy currents induced in the the cryogen which would degrade image quality.
Safety of MRI
MRI is generally considered safe. Since MRI does not use ionizing radiation. Nevertheless, a number potential safety issues concerning MRI must be raised, some related to potential direct effects on the patient from the imaging environment and others related to indirect hazards
Static Field Effects
The most obvious safety implication is the strength of the magnetic field produced by the scanner. There are three forces associated with exposure to this field: a translational force acting on ferromagnetic objects which are brought close to the scanner (projectile effect), the torque on patient devices/implants, and forces on moving charges within the body, most often observed as a superposition of ECG signal. In the main, sensible safety precautions and the screening of patients means that there are seldom any problems. Of major concern is the re-assessment of medical imaplants and devices deemed safe at 1.5 Tesla which may not have been tested at higher fields. This is becoming an issue as 3.0 T scanners become more commonplace.
The extension of the magnetic field beyond the scanner is called the fringe field. All modern scanners incorporate additional coil windings which restrict the field outside of the imaging volume. It is mandatory to restrict public access within the 5 Gauss line, the strength at which the magnetic field interfers with pacemakers.
Gradient Effects
These come under the term 'dB/dt' effects referring to the rate of change in field strength due to gradient switching. The faster the gradients can be turned on and off, the quicker the MR image can be acquired. At 60 T/s peripheral nerve stimulation can occurr, which although harmless may be painful. Cardiac stimulation ocurrs well above this threshold. Manufacturers now employ other methods of increasing imaging speed (so called 'parrallel imaging') in which some gradient encoding is replaced.
RF Heating Effects
The repetitive use of RF pulses deposits energy which in turn causes heating in the patient. This is expressed in terms of SAR (specific absorption rate in W/kg) and is monitored by the scanner computer. For fields up to 3.0 Tesla, the value of SAR is proportional to the square of the field but at high fields the body becomes increasingly conductive neccessitating the use increased RF power. Minor patient burns have resulted from use of high SAR scans plus some other contributory effect, e.g. adverse patient or coil-lead positioning, but this is still a rare event.
Noise
The scans themselves can be quite noisey. The Lorentz forces acting on the gradient coils due to current passing through them in the presence of the main field causes them to vibrate. These mechanical vibrations are transmitted through to the patient as acoustic noise. As a consequence patients must wear earplugs or head phones while being scanned. Again, this effect (actually the force on the gradients) increases at higher field and manufactures are using techniques to combat this including lining the scanner bore or attaching the gradient coils to the scan room floor thereby limiting the degree of vibration.

Claustrophobia
Depending on the mode of entry into the scanner (e.g. head first or feet first) various sites have reported that between 1 % and 10 % of patients experience some degree of claustrophobia which in the extreme cases results in their refusal to proceed with the scan. Fortunately, modern technology means that scanners are becoming wider and shorter drastically reducing this problem for the patient. In addition, bore lighting, ventilation as well as the playing of music all help to reduce this problem to a minimum.
Bioeffects
There are no known or expected harmful effects on humans using field strengths up to 10 Tesla. At 4 Tesla some unpleasant effects have been anedoctally reported including vertigo, flashing lights in the eyes and a metallic taste in the mouth. Currently pregnant women are normally excluded from MRI scans during the first trimester although there is no direct evidence to support this restriction. The most invasive MR scans involve the injection of contrast agents (e.g. Gd-DTPA). This is a colourless liquid that is administered i.v. and has an excellent safety record. Minor reactions like warm sensation at the site of injection or back pain are infrequent and more extreme reactions are very rare.

Summary
MRI uses magnetism and radio frequencies (RF) to create diagnostic sectional images of the body. If the nucleus is spinning, it has angular momentum, or nuclear magnetic moment. This rotating charge acts as a current loop and produces a magnetic field. When a rotating nucleus is subjected to a magnetic field, it will begin to precess. MR imaging is accomplished through various measurements of this movement of the nuclear magnetic field.
The frequency of procession is called the larmor frequency and is critical to MR imaging. Production of the nuclear magnetic resonace signal requires applying a larmor frequency alternating RF and then listening to the RF emissions from the proton. Digital Imaging reconstruction techniques are then used to create sectional and three-dimensional images.
The primary parameters used to modify and control the MRI process include proton spin density, repetition time (TR), echo time (TE), inversion time (TI), T1 and T2. The parameter that are used vary depending on the pulse sequence used. The RF signal strength determines brightness, although it is also affected by field strength, section thickness, the MRI parameter, motion, spatial resolution, S/N, and scan time.