COMPUTERS FUNDAMENTALS AND APPLICATIONS IN MEDICAL IMAGING

COMPUTERS FUNDAMENTALS AND APPLICATIONS IN MEDICAL IMAGING
By ; Sumarsono


The Progressive and evolutionary growth in medicine would not be possible without the aid of computers. As a result of the applications of the computer in the storage, analysis, and manipulation of data, pathologic conditions can be diagnosed more accurately and earlier in the disease process, resulting in an increased patient cure rate. The increasing use of computers in medical science clearly demonstrates the need for qualified personnel who can understand and operate computerized equipment.



History of computer
History of computer could be traced back to the effort of man to count large numbers. This process of counting of large numbers generated various systems of numeration like Babylonian system of numeration, Greek system of numeration, Roman system of numeration and Indian system of numeration. Out of these the Indian system of numeration has been accepted universally. It is the basis of modern decimal system of numeration (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Later you will know how the computer solves all calculations based on decimal system. But you will be surprised to know that the computer does not understand the decimal system and uses binary system of numeration for processing.
1. Calculating Machines
It took over generations for early man to build mechanical devices for counting large numbers. The first calculating device called ABACUS was developed by the Egyptian and Chinese people. The word ABACUS means calculating board. It consisted of sticks in horizontal positions on which were inserted sets of pebbles. A modern form of ABACUS is given in Fig. 1.2. It has a number of horizontal bars each having ten beads. Horizontal bars represent units, tens, hundreds, etc.
2. Napier’s bones
English mathematician John Napier built a mechanical device for the purpose of multiplication in 1617 A D. The device was known as Napier’s bones.
3. Slide Rule
English mathematician Edmund Gunter developed the slide rule. This machine could perform operations like addition,. subtraction, multiplication, and division. It was widely used in Europe in 16th century.
4. Pascal's Adding and Subtractory Machine
You might have heard the name of Blaise Pascal. He developed a machine at the age of 19 that could add and subtract. The machine consisted of wheels, gears and cylinders.
5. Leibniz’s Multiplication and Dividing Machine
The German philosopher and mathematician Gottfried Leibniz built around 1673 a mechanical device that could both multiply and divide.
6. Babbage’s Analytical Engine
It was in the year 1823 that a famous English man Charles Babbage built a mechanical machine to do complex mathematical calculations. It was called difference engine. Later he developed a general-purpose calculating machine called analytical engine. Charles Babbage is called the father of computer.
7. Mechanical and Electrical Calculator
In the beginning of 19th century. The mechanical calculator was developed to perform all sorts of mathematical calculations. Up to the 1960s it was widely used. Later the rotating part of mechanical calculator was replaced by electric motor. So it was called the electrical calculator.

8. Modern Electronic Calculator
The electronic calculator used in 1960 s was run with electron tubes, which was quite bulky. Later it was replaced with transistors and as a result the size of calculators became too small. The modern electronic calculator can compute all kinds of mathematical computations and mathematical functions. It can also be used to store some data permanently. Some calculators have in-built programs to perform some complicated calculations.
Computers that used vacuum tubess as their electronic elements were in use throughout the 1950s. Vacuum tube electronics were largely replaced in the 1960s by transistor-based electronics, which are smaller, faster, cheaper to produce, require less power, and are more reliable. In the 1970s, integrated circuit technology and the subsequent creation of microprocessors, such as the Intel 4004, further decreased size and cost and further increased speed and reliability of computers. By the 1980s, computers became sufficiently small and cheap to replace simple mechanical controls in domestic appliances such as washing machines. The 1980s also witnessed home computers and the now ubiquitous personal computer. With the evolution of the Internet, personal computers are becoming as common as the television and the telephone in the household.
Functional Components of a Computer
The term hardware is used to describe the functional equipment components of a computer and is everything concerning the computer that is visible. Software designates the parts of the computer system that are invisible, such as the machine language and the programs. A computer program may run from just a few instructions to many millions of instructions. A typical modern computer can execute billions of instructions per second (gigahertz or GHz) and rarely make a mistake over many years of operation. Large computer programs comprising several million instructions may take teams of programmers years to write, thus the probability of the entire program having been written without error is highly unlikely.
The computer hardware consist of four functionally independent components : the arithmetic and logic unit (ALU), the control unit, the memory, and the input and output devices (collectively termed I/O). These parts are interconnected by busses, often made of groups of wires.
Input devices is the process of entering data and programs in to the computer system. Computer is an electronic machine like any other machine which takes as inputs raw data and performs some processing giving out processed data. Therefore, the input unit takes data from user to the computer in an organized manner for processing.

The control unit (often called a control system or central controller) directs the various components of a computer. It reads and interprets (decodes) instructions in the program one by one. The control system decodes each instruction and turns it into a series of control signals that operate the other parts of the computer.Control systems in advanced computers may change the order of some instructions so as to improve performance. A key component common to all CPUs is the program counter, a special memory cell (a register) that keeps track of which location in memory the next instruction is to be read from. The control system's function is as follows—note that this is a simplified description, and some of these steps may be performed concurrently or in a different order depending on the type of CPU:
1. Read the code for the next instruction from the cell indicated by the program counter.
2. Decode the numerical code for the instruction into a set of commands or signals for each of the other systems.
3. Increment the program counter so it points to the next instruction.
4. Read whatever data the instruction requires from cells in memory (or perhaps from an input device). The location of this required data is typically stored within the instruction code.
5. Provide the necessary data to an ALU or register.
6. If the instruction requires an ALU or specialized hardware to complete, instruct the hardware to perform the requested operation.
7. Write the result from the ALU back to a memory location or to a register or perhaps an output device.
8. Jump back to step (1).

The process of saving data and instructions permanently is known as storage. Data has to be fed into the system before the actual processing starts. It is because the processing speed of Central Processing Unit (CPU) is so fast that the data has to be provided to CPU with the same speed. Therefore the data is first stored in the storage unit for faster access and processing. This storage unit or the primary storage of the computer system is designed to do the above functionality. It provides space for storing data and instructions.
Computer main memory comes in two principal varieties: random access memory or RAM and read-only memory or ROM. RAM can be read and written to anytime the CPU commands it, but ROM is pre-loaded with data and software that never changes, so the CPU can only read from it. ROM is typically used to store the computer's initial start-up instructions. In general, the contents of RAM is erased when the power to the computer is turned off while ROM retains its data indefinitely. In a PC, the ROM contains a specialized program called the BIOS that orchestrates loading the computer's operating system from the hard disk drive into RAM whenever the computer is turned on or reset. In embedded computers, which frequently do not have disk drives, all of the software required to perform the task may be stored in ROM. Software that is stored in ROM is often called firmware because it is notionally more like hardware than software. Flash memory blurs the distinction between ROM and RAM by retaining data when turned off but being rewritable like RAM. However, flash memory is typically much slower than conventional ROM and RAM so its use is restricted to applications where high speeds are not required.In more sophisticated computers there may be one or more RAM cache memories which are slower than registers but faster than main memory. Generally computers with this sort of cache are designed to move frequently needed data into the cache automatically, often without the need for any intervention on the programmer's part.
The ALU is capable of performing two classes of operations: arithmetic and logic. The set of arithmetic operations that a particular ALU supports may be limited to adding and subtracting or might include multiplying or dividing, trigonometry functions (sine, cosine, etc) and square roots. Some can only operate on whole numbers (integers) whilst others use floating point to represent real numbers—albeit with limited precision. However, any computer that is capable of performing just the simplest operations can be programmed to break down the more complex operations into simple steps that it can perform. Therefore, any computer can be programmed to perform any arithmetic operation—although it will take more time to do so if its ALU does not directly support the operation. An ALU may also compare numbers and return boolean truth values (true or false) depending on whether one is equal to, greater than or less than the other .
Output: This is the process of producing results from the data for getting useful information. Similarly the output produced by the computer after processing must also be kept somewhere inside the computer before being given to in human readable form. Again the output is also stored inside the computer for further processing.
Binary System
In computer’s memory both programs and data are stored in the binary form. The binary system has only two values 0 and 1. As human beings we all understand decimal system but the computer can only understand binary system. It is because a large number of integrated circuits inside the computer can be considered as switches, which can be made ON, or OFF. If a switch is ON it is considered 1 and if it is OFF it is 0. A number of switches in different states will give a message like : 110101....10. So the computer takes input in the form of 0 and 1 and gives output in the form 0 and 1 only. Every number in binary system can be converted to decimal system and vice versa; for example, 1010 meaning decimal 10. Therefore it is the computer that takes information or data in decimal form from user, convert it in to binary form, process it producing output in binary form and again convert the output to decimal form.
In almost all modern computers, each memory cell is set up to store binary numbers in groups of eight bits (called a byte). Each byte is able to represent 256 different numbers; either from 0 to 255 or -128 to +127. To store larger numbers, several consecutive bytes may be used (typically, two, four or eight). When negative numbers are required, they are usually stored in two's complement notation. Other arrangements are possible, but are usually not seen outside of specialized applications or historical contexts. A computer can store any kind of information in memory as long as it can be somehow represented in numerical form. Modern computers have billions or even trillions of bytes of memory.
Applications in Medical Imaging
Analog to Digital Converters
Devices that produce images of real objects, such as patients, produce an analog rather than digital signal. The electrical signal being emitted from the output phosphor of an image intensifier on a fluoroscopic unit, the scintillation crystal of a nuclear medicine detector of a computed tomography (CT) unit, or the piezoelectric crystal of an ultrasound machine is in analog form with a variance in voltage. For these signals to be read as data by the computer, they must by digitized an converted into binary numbers system. The peripheral device that performs this task is the analog-to-digital converter, which transforms the sine wave into discrete increments with binary numbers assigned to each increment. The assignment of the binary numbers depends on output voltage, which in turn represents the degree of attenuation of the various tissue densities within the patient. The basic component of an analog digital converter (ADC) is the “comparator” that outputs a “1” when the voltage equals or exceeds a precise analog voltage and a “0” if the voltage does not equal or exceed this predetermined level. The most significant parameters of an ADC are (1) digitization depth (the number of bits in the resultant binary number); (2) dynamic range (the range of voltage or input signals the result in a digital output); (3) digitization rate (the rate that digitization takes place). Achieving the optimal digitization depth is necessary for resolution quality and flexibility in image manipulation. Digitization depth and dynamic range are analogous and latitude in a radiograph.

To produce a video image, the field size of the image is divided into many cubes or matrix, with each cube assigned a binary number proportional to the degree of the attenuation of the x-ray beam or intensity of the incoming signal. The individual three-dimensional cubes with length, width, and depth are called voxel (volume element), with the degree of attenuation or intensity of the incoming voltage determining their composition and thickness.

Because the technology for displaying three-dimensional objects has not been fully developed, a two-dimensional square or pixel (picture element) represent the voxel on the television display monitor or cathode ray tube. The matrix is an array of pixel arranged in two dimension, length and width, or in row and columns. The more pixel contained in a image, the larger matrix becomes, with the resolution quality of the image improving. For instance, a matrix containing 256 x 256 pixels has atotal of 65,536 pixel or pieces of data; whereas a matrix of 512 x 512 pixels contains 262,144 pieces of data. One should not confuse field size with matrix size. The larger matrix also allows for more manipulation of the data or the image displayed on the television monitor and is very beneficial and useful in the imaging modalities, such as digital substraction fluoroscopy, CT, nuclear medicine, and ultrasound.

DIGITAL IMAGING PROCESSING

Digital image processing is the use of computer algorithms to perform image processing on digital images. As a subfield of digital signal processing, digital image processing has many advantages over analog image processing; it allows a much wider range of algorithms to be applied to the input data, and can avoid problems such as the build-up of noise and signal distortion during processing

Within the computer system, digital images are represented as groups of numbers. Therefore these numbers can be changed through applying mathematic operations, and the result the images is altered, this important concept has provide extraordinary control in contrast enhancement, image enhancement, subtraction techniques, and magnification without losing the original image data.
Contrast Enhancement
Window width encompasses the range densities within an image. A narrow window is comparable to the use of a high-contrast radiographic film. As a result, image contrast is increased. Increasing the width of the window allows more of the gray scale to be visualized or more latitude in the densities of the image visualized. A narrow window is valuable when subtle differences in subject density need to be better visualized. However, the use of a narrow window increases image noise, and densities outside of the narrow window are not visualized.

Image Enhancement or Reconstruction
Image enhancement or reconstruction is accomplished by the use of digital processing of filtering, which can be defined as accenting or attenuating selected frequencies in the image. The filtration methods used in the medical imaging are classified as (1) convolution; (2) low-pass-filtering or smoothing; (3) band-pass filtering; and (4) high-pass filtering, or edge’ enhancement. The background intensities within a medical image consist mainly of low spatial frequencies, whereas an edge, typifying a sudden change in intensities, is composed of mainly high spatial frequencies for example, the bone-to-air interface or the skull when using computed tomography. Spatial noise originating from within the computer system is usually high spatial frequencies. Filtration reduces the amount of high spatial frequencies inherent in the object. The percentage of transmission versus spatial frequency, if ploted on a graph, called modulation transfer function (MTF). One effort of continuing research in medical imaging is a develop systems with higher modulation transfer function.

Convolution is accomplished automatically with computer system that are equipped with fast fourier transforms, the convolutions process is implemented by placing a filter mask array, or matrix, over the image array, or matrix, in the memory. A filter mask is a square array or section with numbers, usually consisting of an area of 3 x 3 elements. The size of the filter mask is determined by the manufacturer of the equipment, although larger mask are not often used because they take longer to process. The convolution filtering process can be conceptualized as placing the filter mask over an area of the image marix, multipliying each element value direcly beneath it, obtaining a sum of these values, and then placing that sum within the output image in the exact location as it was in the original image.

Subtraction Technique
The advantages of using digital substraction include the ability to visualize small anatomic structures and to perform the examination via venous injection of contras media. The most common digital subtraction technique are temporal subtraction and dual energy subtraction. Hybrid subtraction is a combination of these two methods.

Magnification
Magnification, sometimes called zooming, is a process of selecting an area of interest and copying each pixel within the area an integer number of times. Large magnifications may give the image an appearance of being constructed of blocks. To provide a more diagnostic image, a smoothing or low-pass filter operation can be done to smooth out the distinct intensities between the blocks.

Three-Dimensional Image
When three dimensional imaging was first introduced, the images were less than optimal because of the resolution being too low to adequately visualize anatomic structures deeper within the body. The images often adequately displayed only the more dense structures closer to the body surface, or surface boundaries, which appeared blocky and jagged; therefore, the soft tissue or less dense structures were not visualized. By using fast Fourier transforms (3DFT), new algorithms for mathematical calculations, and development of computers with faster processing time, three dimensional images have become smooth, sharply focused, and realistically shaded to demonstrate soft tissue. The ability to demonstrate soft tissue in three dimensional imaging is referred to as a volumetric rendering technique.

Volumetric rendering is a computer program whereby “stack” of sequential images are processed as a volume with the gray scale intensity information in each pixel being interpolated in the z axis (perpendicular to to the x and y axes). Interpolated is necessary because the field of view of the scan (the x and y axes). is not the same as the z axis because of interscan spacing. Following this computer process, new data are generated by interpolation, resulting in each new voxel having all the same dimension. The volumetric rendering technique enables definitions of the object’s thickness, a crucial factor in three dimensional imaging and in visualizing subtle densities.

Read More..

THE BASIC PRINCIPLES OF ULTRASONOGRAPHY (USG)

THE BASIC PRINCIPLES OF ULTRASONOGRAPHY (USG)
By : Sumarsono


Diagnostic Ultrasonography sometimes called “diagnostic medical sonography” has become a clinically valuable imaging technique. It differs from diagnostic radiology in that it uses nonionizing, high-frequency sound waves to generate an image of a particular structure. Ultrasound is employed in the visualization of muscles, tendons, and many internal organs, their size, structure and any pathological lesions with real time tomographic images.. Blood velocities may be calculated in vascular and cardiac structures with the Doppler technique.The Ultrasound equipment may be easily moved into the operating room, special care nursery, or intencive care unit or may be manually transported by means of a mobile van service to provide ultrasound service for smaller hospital and clinics. Ultrasound is cost-effective compared with computed tomography (CT), magnetic resonance imaging (MRI), or angiography.Further development in high-frequency, millimeter size tranducers mounted on the tip of an angiographic catheter (IVUS; Intra Vascular Ultrasound) have great potential.


History

Physical Principles
Ultrasound is sound waves greater than 20,000 Hertz (greater than the upper limit of human hearing). The audible sound frequencies are below 15 000 to 20 000 Hz, while frequency ranges used in medical ultrasound imaging are 2 -15 MHz. Audible sound travels around corners, the human can hear sounds around a corner (sound diffraction). With higher frequencies the sound tend to move more in straight lines like electromagnetic beams, and will be reflected like light beams. They will be reflected by much smaller objects (because of sorter wavelengths), and does not propagate easily in gaseous media. At higher frequencies the ultrasound behaves more like electromagnetic radiation. The wavelength is inversely related to the frequency f by the sound velocity c:
c = λf
Meaning that the velocity equals the wavelength times the number of oscillations per second, and thus:

λ =c/f

The sound velocity i a given material is constant (at a given temperature), but varies in different materials :



The speed of sound is different in different materials, and is dependent on the acoustical impedance of the material. However, the sonographic instrument assumes that the acoustic velocity is constant at 1540 m/s. An effect of this assumption is that in a real body with non-uniform tissues, the beam becomes somewhat de-focused and image resolution is reduced.

Basically, all ultrasound imaging is performed by emitting a pulse, which is partly reflected from a boundary between two tissue structures, and partially transmitted. The reflection depends on the difference in impedance of the two tissues.
The ratio of the amplitude (energy) of the reflected pulse and the incident is called the reflection coefficient. The ratio of the amplitude of the incident pulse and the transmitted pulse is called the transmission coefficient. Both are dependent on the differences in acoustic impedance of the two materials. The acoustic impedance of a medium is the speed of sound in the material × the density:
Z = c ×

The reflecting structures does not only reflect directly back to the transmitter, but scatters the ultrasound in more directions. Thus, the reflecting structures are usually termed scatterers.


The time lag, , between emitting and receiving a pulse is the time it takes for sound to travel the distance to the scatterer and back, i.e. twice the range, r, to the scatterer at the speed of sound, c, in the tissue. Thus:

r = cτ / 2

The pulse is thus emitted, and the system is set to await the reflected signals, calculating the depth of the scatterer on the basis of the time from emission to reception of the signal. The total time for awaiting the refelcted ultrasound is determined by the preset depth desired in the image.
Piezoelectric effect
Ultrasound is generated by piezoelectric crystals that vibrates when compressed and decompressed by an alternating current applied across the crystal, the same crystals can act as receivers of reflected ultrasound, the vibrations induced by the ultrasound pulse .
Piezoelectric effect , voltage produced between surfaces of a solid dielectric (nonconducting substance) when a mechanical stress is applied to it. A small current may be produced as well. The effect, discovered by Pierre Curie in 1883, is exhibited by certain crystals, e.g., quartz and Rochelle salt, and ceramic materials. When a voltage is applied across certain surfaces of a solid that exhibits the piezoelectric effect, the solid undergoes a mechanical distortion. Piezoelectric materials are used in transducers , e.g., phonograph cartridges, microphones, and strain gauges, which produce an electrical output from a mechanical input, and in earphones and ultrasonic radiators, which produce a mechanical output from an electrical input. Piezoelectric solids typically resonate within narrowly defined frequency ranges; when suitably mounted they can be used in electric circuits as components of highly selective filters or as frequency-control devices for very stable oscillators .
Transducer
A sound wave is typically produced by a piezoelectric transducer encased in a probe. Strong, short electrical pulses from the ultrasound machine make the transducer ring at the desired frequency.The sound is focused either by the shape of the transducer, a lens in front of the transducer, or a complex set of control pulses from the ultrasound scanner machine. This focusing produces an arc-shaped sound wave from the face of the transducer. The wave travels into the body and comes into focus at a desired depth. A probe containing one or more acoustic transducers to send pulses of sound into the body. Whenever a sound wave encounters a material with a different density (acoustical impedance), part of the sound wave is reflected back to the probe and is detected as an echo. The time it takes for the echo to travel back to the probe is measured and used to calculate the depth of the tissue interface causing the echo. The greater the difference between acoustic impedances, the larger the echo is. If the pulse hits gases or solids, the density difference is so great that most of the acoustic energy is reflected and it becomes impossible to see deeper.
Older technology transducers focus their beam with physical lenses. Newer technology transducers use phased array techniques to enable the sonographic machine to change the direction and depth of focus. Almost all piezoelectric transducers are made of ceramic.
Materials on the face of the transducer enable the sound to be transmitted efficiently into the body (usually seeming to be a rubbery coating, a form of impedance matching). In addition, a water-based gel is placed between the patient's skin and the probe.
The sound wave is partially reflected from the layers between different tissues. Specifically, sound is reflected anywhere there are density changes in the body: e.g. blood cells in blood plasma, small structures in organs, etc. Some of the reflections return to the transducer.



To generate a 2D-image, the ultrasonic beam is swept. A transducer may be swept mechanically by rotating or swinging. Or a 1D phased array transducer may be use to sweep the beam electronically. The received data is processed and used to construct the image. The image is then a 2D representation of the slice into the body.
3D images can be generated by acquiring a series of adjacent 2D images. Commonly a specialised probe that mechanically scans a conventional 2D-image transducer is used. However, since the mechanical scanning is slow, it is difficult to make 3D images of moving tissues. Recently, 2D phased array transducers that can sweep the beam in 3D have been developed. These can image faster and can even be used to make live 3D images of a beating heart.
Doppler ultrasonography is used to study blood flow and muscle motion. The different detected speeds are represented in color for ease of interpretation, for example leaky heart valves: the leak shows up as a flash of unique color. Colors may alternatively be used to represent the amplitudes of the received echoes.
Display Modes
Four different modes of ultrasound are used in medical imaging. These are:
• A-mode (amplitude modulation) : A-mode is the simplest type of ultrasound. The received energy at a certain time, i.e. from a certain depth, can be displayed as energy amplitude. The greater the reflection at the interface, the larger the signal amplitude will appear on the A-mode screen.


• B-mode (Brightness) : The amplitude can also be displayed as the brightness of the certain point representing the scatterer. In B-mode ultrasound, a linear array of transducers simultaneously scans a plane through the body that can be viewed as a two-dimensional image on screen.

• M-mode (motion mode) : if some of the scatterers are moving, the motion curve can be traced In m-mode a rapid sequence of B-mode scans whose images follow each other in sequence on screen enables to see and measure range of motion, as the organ boundaries that produce reflections move relative to the probe.

• D Mode or Doppler mode: This mode makes use of the Doppler effect. The Doppler information is displayed graphically using spectral Doppler, or as an image using color Doppler (directional Doppler) or power Doppler (non directional Doppler). This Doppler shift falls in the audible range and is often presented audibly using stereo speakers: this produces a very distinctive, although synthetic, pulsing sound.

Artifacts
Artifacts is Portions of the display which are not a “true” representation of the tissue imaged. Medical Diagnostic Ultrasound imaging utilizes certain artifacts to characterize tissue.The ability to differentiate solid vs. cystic tissue is the hallmark of ultrasound imaging. Acoustic shadowing and acoustic enhancement are the two artifacts that provide the most useful diagnostic information. Acoustic shadowing diminished sound or loss of sound posterior to a strongly reflecting (e.g.,large calcifications, bone) or strongly attenuating structure (solid tissue, significantly dense or malignant masses).

Acoustic enhancement is the increased of transmission of the sound wave posterior to a weakly attenuating structure (e.g., simple cysts or weakly attenuating masses). Gain curve expected a certain loss or attenuating with depth of travel.

Diagnostic applications
A general-purpose sonographic machine may be able to be used for most imaging purposes. Usually specialty applications may be served only by use of a specialty transducer. The dynamic nature of many studies generally requires specialized features in a sonographic machine for it to be effective; such as endovaginal, endorectal, or transesophageal transducers.
Obstetrical ultrasound is commonly used during pregnancy to check on the development of the fetus. In a pelvic sonogram, organs of the pelvic region are imaged. This includes the uterus and ovaries or urinary bladder. Men are sometimes given a pelvic sonogram to check on the health of their bladder and prostate. There are two methods of performing a pelvic sonography - externally or internally. The internal pelvic sonogram is performed either transvaginally (in a woman) or transrectally (in a man). Sonographic imaging of the pelvic floor can produce important diagnostic information regarding the precise relationship of abnormal structures with other pelvic organs and it represents a useful hint to treat patients with symptoms related to pelvic prolapse, double incontinence and obstructed defecation.
In abdominal sonography, the solid organs of the abdomen such as the pancreas, aorta, inferior vena cava, liver, gall bladder, bile ducts, kidneys, and spleen are imaged. Sound waves are blocked by gas in the bowel, therefore there are limited diagnostic capabilities in this area. The appendix can sometimes be seen when inflamed eg: appendicitis

Read More..

THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING (MRI)

THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING
(MRI
By : Sumarsono


History
Felix Bloch and Edward Purcell, both of whom were awarded the Nobel Prize in 1952, discovered the magnetic resonance phenomenon independently in 1946. In the period between 1950 and 1970, NMR was developed and used for chemical and physical molecular analysis.
In 1971 Raymond Damadian showed that the nuclear magnetic relaxation times of tissues and tumors differed, thus motivating scientists to consider magnetic resonance for the detection of disease. Magnetic resonance imaging was first demonstrated on small test tube samples that same year by Paul Lauterbur. He used a back projection technique similar to that used in CT. In 1975 Richard Ernst proposed magnetic resonance imaging using phase and frequency encoding, and the Fourier Transform This technique is the basis of current MRI techniques. A few years later, in 1977, Raymond Damadian demonstrated MRI called field-focusing nuclear magnetic resonance. In this same year, Peter Mansfield developed the echo-planar imaging (EPI) technique. Edelstein and coworkers demonstrated imaging of the body using Ernst's technique in 1980. A single image could be acquired in approximately five minutes by this technique. By 1986, the imaging time was reduced to about five seconds, without sacrificing too much image quality. The same year people were developing the NMR microscope, which allowed approximately 10 mm resolution on approximately one cm samples. In 1987 echo-planar imaging was used to perform real-time movie imaging of a single cardiac cycle. In this same year Charles Dumoulin was perfecting magnetic resonance angiography (MRA), which allowed imaging of flowing blood without the use of contrast agents.



In 1991, Richard Ernst was rewarded for his achievements in pulsed Fourier Transform NMR and MRI with the Nobel Prize in Chemistry. In 1992 functional MRI (fMRI) was developed. This technique allows the mapping of the function of the various regions of the human brain. Five years earlier many clinicians thought echo-planar imaging's primary applications was to be in real-time cardiac imaging. The development of fMRI opened up a new application for EPI in mapping the regions of the brain responsible for thought and motor control. In 1994, researchers at the State University of New York at Stony Brook and Princeton University demonstrated the imaging of hyperpolarized 129Xe gas for respiration studies. In 2003, Paul C. Lauterbur of the University of Illinois and Sir Peter Mansfield of the University of Nottingham were awarded the Nobel Prize in Medicine for their discoveries concerning magnetic resonance imaging. MRI is clearly a young, but growing science.
The Basic Physics
The human body is primarily fat and water. Fat and water have many hydrogen atoms which make the human body approximately 63% hydrogen atoms. Hydrogen nuclei have an NMR signal. For these reasons magnetic resonance imaging primarily images the NMR signal from the hydrogen nuclei. Each voxel of an image of the human body contains one or more tissues. Within each cell there are water molecules. Each water molecule has one oxygen and two hydrogen atoms. One hydrogen atom contain one proton (single proton).

THE BASIC PRINCIPLES OF MAGNETIC RESONANCE IMAGING
(MRI)
Spin
The proton possesses a property called spin which: it can be thought of as a small magnetic field, and will cause the nucleus to produce an NMR signal.

Spin is a fundamental property of nature like electrical charge or mass. Spin comes in multiples of 1/2 and can be + or -. Protons, electrons, and neutrons possess spin. Individual unpaired electrons, protons, and neutrons each possesses a spin of 1/2. In the deuterium atom ( 2H ), with one unpaired electron, one unpaired proton, and one unpaired neutron, the total electronic spin = 1/2 and the total nuclear spin = 1. Two or more particles with spins having opposite signs can pair up to eliminate the observable manifestations of spin. An example is helium. In nuclear magnetic resonance, it is unpaired nuclear spins that are of importance. Spin of proton like a magnetic moment vector, causing the proton to behave like a tiny magnet with a north (N) and south pole (S).
A collection of 1H nuclei (spinning protons) in the absence of an externally applied magnetic field. The magnetic moments have random orientations.When the proton is placed in an external magnetic field B0, the spin vector of the particle aligns itself with the external field, one of two orientations with respect to B0 (denoted parallel and anti-parallel). Protons aligned in the parallel orientation are said to be in a low energy state. Protons in the anti-parallel orientation are said to be in a high-energy state.

The energy differential between the high and low energy states is proportional to the strength of the externally applied magnetic field B0. Also related to the strength of B0 is the number of spins in the low energy state. The higher the B0, the greater the number of spins aligned in the low-energy state. The number of spins in the low energy state in excess of the number in the high-energy state is referred to as the spin excess. The magnetic moments of these excess spins add to form the net magnetization and thus the tissue placed in the magnetic field becomes magnetized. The net magnetization is also represented as a vector quantity. As previously mentioned, a larger B0 will produce a greater spin excess. Therefore, a larger B0 will produce a larger net magnetization vector.
Larmor’s Formula
The spin vektor do not line up precisely with external magnetic field but at an angle to the field, and they rotate about the direction of the magnetic field similar to the wobbling motion of a spinning top. This wobbling motion is called precession and occurs at a specific frequency (rate) for a given atom’s nucleus in a magnetic field of a specific strenght.
The Larmor equation expresses the relationship between the strength of a magnetic field, B0, and the precessional frequency, ωo, of an individual spin. From The Larmor Equation that the precessional frequency is equal to the strength of the external static magnetic field (B0) multiplied by the gyromagnetic ratio (γ). Increasing B0 will increase the precessional frequency and conversely, decreasing B0 will decrease the precessional frequency. This is analogous to a spinning top. It will precess due to the force of gravity. If the gravity were to be decreased (as it is on the moon), then the top would precess slower.
Wo = γ BO
The proportionality constant to the left of B0 is known as the gyromagnetic ratio of the nucleus. The precessional frequency, ωo, is also known as the Larmor frequency. For a hydrogen nucleus, the gyromagnetic ratio is 4257 Hz/Gauss. Thus at 1.5 Tesla (15,000 Gauss), ωo = 63.855 Megahertz.



Fourier Transformation
To understand how an image is constructed in MRI it is first instructive to take a look at Fourier Transformation (FT). FT permits signal to be decomposed into a sum of sine waves each of different frequency, phases and amplitudes.

S(t) = a0 + a1sin(1t + 1) + a2sin(2t + 2) + ...
The FT of the signal in the time domain can be represented in the equivalent frequency domain by a series of peaks of various amplitudes. In MRI the signal is spatially encoded by changes of phase/frequency which is then unravelled by performing a 2D FT to identify pixel intensities across the image.

MRI Signal Production
Hydrogen exists in many molecules in the body. Water (consisting of two hydrogen atoms and one oxygen) comprises up to 70% of body weight. Hydrogen is also present in fat and most other tissues in the body. The varying molecular structures and the amount of hydrogen in various tissues effect how the protons behave in the external field. As an example, because of the total amount of hydrogen in water, it has one of the strongest net magnetization vectors relative to other tissues. Other structures and tissues within the body have less hydrogen concentration and become magnetized to a lesser extent. In other words, their net magnetization is less intense.
The amount of mobile hydrogen protons that a given tissue possesses, relative to water (specifically CSF), is referred to as its spin density (proton density). This is the basis with which we begin to produce images using Magnetic Resonance. The hydrogen nucleus contains one proton and possesses a significant magnetic moment. In addition, hydrogen is very abundant in the human body. By placing the patient in a large external magnetic field, will magnetize the tissue (hydrogen), preparing it for the MR imaging process.
A radio wave is actually an oscillating electromagnetic field. It is oriented perpendicular to the main magnetic field (B0). If a pulse of RF energy apply into the tissue at the Larmor frequency, the individual spins begin to precess in phase, as will the net magnetization vector. As the RF pulse continues, some of the spins in the lower energy state absorb energy from the RF field and make a transition into the higher energy state. This has the effect of tipping the net magnetization toward the transverse plane.


The angle through which M has rotated away from the z-axis is known as the flip angle. The strength and duration of B1 determine the amount of energy available to achieve spin transitions between parallel and anti-parallel states. Thus, the flip angle is proportional to the strength and duration of B1. Pulses of 90 degrees is applied to produce a 90-degree flip of the net magnetization. A pulse of 180 degrees rotates M into a position directly opposite to B0, with greater numbers of spins adopting anti-parallel (rather than parallel) states. If the B1 field is applied indefinitely, M tilts away from the z-axis, through the x-y plane towards the negative z direction, and finally back towards the x-y plane and z-axis (where the process begins again).
As the magnetization (now referred to as transverse magnetization, or Mxy) precesses through the receiver coil, a current or signal is induced in the coil. The principle behind this signal induction is Faradays Law of Induction. This states that if a magnetic field is moved through a conductor, a current will be produced in the conductor. the increasing the size of the magnetic field, or the speed with which it moves, will increase the size of the signal (current) induced in the conductor .
In order to detect the signal produced in the receiver coil, the transmitter must be turned off. When the RF pulse is discontinued, the signal in the coil begins at a given amplitude (determined by the amount of magnetization precesssing in the transverse plane and the precessional frequency) and fades rapidly away. This initial signal is referred to as the Free Induction Decay or FID

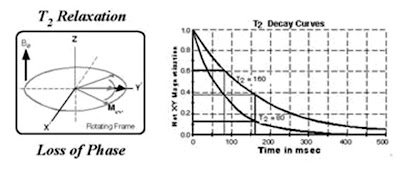
The return of M to its equilibrium state (the direction of the z-axis) is known as relaxation. The signal fades as the individual spins contributing to the net magnetization loose their phase coherence, making the vector sum equal to zero. Flipped nuclei start off all spinning together known as T2 relaxation, but quickly become incoherent (out of phase). The FID decays at a rate given by disturbances in magnetic field (magnetic susceptibility) increase the rate of spin coherence T2 relaxation known as T2* (T2-star). At the same time, but independently, some of the spins that had moved into the higher energy state give off their energy to their lattice and return to the lower energy state, causing the net magnetization to regrow along the z axis. This regrowth occurs at a rate given by the tissue relaxation parameter known as T1. The total NMR signal is a combination of the total number of nuclei (proton density), reduced by the T1, T2, and T2* relaxation components.
Magnet inhomogeneity
It is virtually impossible to construct an NMR magnet with perfectly uniform magnetic field strength, B0. Much additional hardware is supplied with NMR machines to assist in normalising the B0 field. However, it is inevitable that an NMR sample will experience different B0's across its body so that nuclei comprising the sample (that exhibit spin) will have different precessional frequencies (according to the Larmor equation). Immediately following a 90 degree pulse, a sample will have Mx-y coherent. However, as time goes on, phase differences at various points across the sample will occur due to nuclei precessing at different frequencies. These phase differences will increase with time and the vector addition of these phases will reduce Mx-y with time.
T1 relaxation
Following termination of an RF pulse, nuclei will dissipate their excess energy as heat to the surrounding environment (or lattice) and revert to their equilibrium position. Realignment of the nuclei along B0, through a process known as recovery, leads to a gradual increase in the longitudinal magnetisation. The time taken for a nucleus to relax back to its equilibrium state depends on the rate that excess energy is dissipated to the lattice. Let M-0-long be the amount of magnetisation parallel with B0 before an RF pulse is applied. Let M-long be the z component of M at time t, following a 90 degree pulse at time t = 0. It can be shown that the process of equilibrium restoration is described by the equation.



where T1 is the time taken for approximately 63% of the longitudinal magnetisation to be restored following a 90 degree pulse.


T2 relaxation
While nuclei dissipate their excess energy to the lattice following an RF pulse, the magnetic moments interact with each other causing a decrease in transverse magnetisation. This effect is similar to that produced by magnet inhomogeneity, but on a smaller scale. The decrease in transverse magnetisation (which does not involve the emission of energy) is called decay. The rate of decay is described by a time constant, T2*, that is the time it takes for the transverse magnetisation to decay to 37% of its original magnitude. T2* characterises dephasing due to both B0 inhomogeneity and transverse relaxation. Let M-0-trans be the amount of transverse magnetisation (Mx-y) immediately following an RF pulse. Let M-trans be the amount of transverse magnetisation at time t, following a 90 degree pulse at time t = 0. It can be shown that
Mtrans = Motrans.e-t/T2*

In order to obtain signal with a T2 dependence rather than a T2* dependence, a pulse sequence known as the spin-echo has been devised which reduces the effect of B0 inhomogeneity on Mx-y. A pulse sequence is an appropriate combination of one or more RF pulses and gradients (see next section) with intervening periods of recovery. A pulse sequence consists of several components, of which the main ones are the repetition time (TR), the echo time (TE), flip angle, the number of excitations (NEX), bandwidth and acquisition matrix.



The signal intensity
The signal intensity on the MR image is determined by four basic parameters: 1) proton density, 2) T1 relaxation time, 3) T2 relaxation time, and 4) flow. Proton density is the concentration of protons in the tissue in the form of water and macromolecules (proteins, fat, etc). The contrast on the MR image can be manipulated by changing the pulse sequence parameters. A pulse sequence sets the specific number, strength, and timing of the RF and gradient pulses.
The two most important parameters are the repetition time (TR) and the echo time (TE). The TR is the time between consecutive 90 degree RF pulse. The TE is the time between the initial 90 degree RF pulse and the echo. The most common pulse sequences are the T1- weighted and T2-weighted spin-echo sequences. The T1-weighted sequence uses a short TR and short TE (TR < 1000msec, TE < 30msec). The T2-weighted sequence uses a long TR and long TE (TR > 2000msec, TE > 80msec). The T2-weighted sequence can be employed as a dual echo sequence. The first or shorter echo (TE < 30msec) is proton density (PD) weighted or a mixture of T1 and T2. This image is very helpful for evaluating periventricular pathology, such as multiple sclerosis, because the hyperintense plaques are contrasted against the lower signal CSF. More recently, the FLAIR (Fluid Attenuated Inversion Recovery) sequence has replaced the PD image. FLAIR images are T2-weighted with the CSF signal suppressed.


One of the great advantages of MRI is its excellent soft-tissue contrast which can be widely manipulated. In a typical image acquisition the basic unit of each sequence is repeated hundreds of times over. By altering the echo time (TE) or repetition time (TR), i.e. the time between successive 90° pulses, the signal contrast can be altered or weighted. For example if a long TE is used, inherent differences in T2 times of tissues will become apparent. Tissues with a long T2 (e.g. water) will take longer to decay and their signal will be greater (or appear brighter in the image) than the signal from tissue with a short T2 (fat). In a similar manner TR governs T1 contrast. Tissue with a long TR (water) will take a long time to recover back to the equilibrium magnetisation value, so therefore a short TR interval will make this tissue appear dark compared to tissue with a short T1 (fat). When TE and TR are chosen to minimise both these weightings, the signal contrast is only derived from the number or density of spins in a given tissue. This image is said to be 'proton-density weighted'. To summarise:1). T2-weighting requires long TE, long TR 2).T1-weighting requires short TE, short TR 3). PD-weighting requires short TE, long TR
Spatial Localisation
The actual location within the sample from which the RF signal was emitted is determined by superimposing magnetic field gradients on the magnet generating the otherwise homogeneous external magnetic field B0. For example, a magnetic field gradient can be superimposed by placing two coils of wire (wound in opposite directions) around the B0 field with longitudinal axis orientated in the z direction and then by passing direct current through the coils. The magnetic field from the coil pair adds to the B0 field, with the result that one end of the magnet has a higher field strength than the other known as magnetic gradient. According to the Larmor equation, the magnetic field gradient causes identical nuclei to precess at different Larmor frequencies. The frequency deviation is proportional to the distance of the nuclei from the centre of the gradient coil and the current flowing through the coil.


Slice Selection

Frequency Encoding
Three magnetic field gradients, placed orthogonally to one another inside the bore of the magnet, are required to encode information in three dimensions. With a slice selected and excited as described in the previous paragraph, current is switched to one of the two remaining gradient coils (referred to as the frequency encoding gradient). This has the effect of spatially encoding the excited slice along one axis, so that columns of spins perpendicular to the axis precess at slightly different Larmor frequencies. For a homogeneous sample, the intensity of the signal at each frequency is proportional to the number of protons in the corresponding column.
The frequency encoding gradient is turned on just before the receiver is gated on and is left on while the signal is sampled or read out. For this reason the frequency encoding gradient is also known as the readout gradient. The resulting FID is a graph of signal (formed from the interference pattern of the different frequencies) induced in the receiver verses time. If the FID is subjected to Fourier transform, a conventional spectrum in which signal amplitude is plotted as a function of frequency can be obtained. Thus, a graph of signal verses frequency is obtained which corresponds to a series of lines or views representing columns of spins in the slice.
Phase Encoding
Suppose a slice through a homogeneous sample has been selected and excited as described in Slice Selection section, and then frequency encoded according to the previous section. After a short time, the phase of the spins at one end of the gradient leads those at the other end because they are precessing faster. If the frequency encoding gradient is switched off, spins precess (once more) at the same angular velocity but with a retained phase difference. This phenomenon is known as phase memory.
A phase encoding gradient is applied orthogonally to the other two gradients after slice selection and excitation, but before frequency encoding. The phase encoding gradient does not change the frequency of the received signal because it is not on during signal acquisition. It serves as a phase memory, remembering relative phase throughout the slice.
To construct a 256 x 256 pixels image a pulse sequence is repeated 256 times with only the phase encoding gradient changing. The change occurs in a stepwise fashion, with field strength decreasing until it reaches zero, then increasing in the opposite direction until it reaches its original amplitude. At the end of the scan, 256 lines (one for each phase encoding step) comprising 256 samples of frequency are produced. A Fourier transformation allows phase information to be extracted so that a pixel (x, y) in the slice can be assigned the intensity of signal which has the correct phase and frequency corresponding to the appropriate volume element. The signal intensity is then converted to a grey scale to form an image.

MRI Sequences
MRI signal intensity depends on many parameters, including proton density, T1 and T2 relaxation times. Different pathologies can be selected by the proper choice of pulse sequence parameters. Repetition time (TR) is the time between two consecutive RF pulses measured in milliseconds. For a given type of nucleus in a given environment, TR determines the amount of T1 relaxation. The longer the TR, the more the longitudinal magnetisation is recovered. Tissues with short T1 have greater signal intensity than tissues with a longer T1 at a given TR. A long TR allows more magnetisation to recover and thus reduces differences in the T1 contribution in the image contrast. Echo time (TE) is the time from the application of an RF pulse to the measurement of the MR signal. TE determines how much decay of the transverse magnetisation is allowed to occur before the signal is read. It therefore controls the amount of T2 relaxation. The application of RF pulses at different TRs and the receiving of signals at different TEs produces variation in contrast in MR images. Next some common MRI sequences are described.
Spin Echo Pulse Sequence
The spin echo (SE) sequence is the most commonly used pulse sequence in clinical imaging. The sequence comprises two radiofrequency pulses - the 90 degree pulse that creates the detectable magnetisation and the 180 degree pulse that refocuses it at TE. The selection of TE and TR determines resulting image contrast. In T1-weighted images, tissues that have short T1 relaxation times (such as fat) present as bright signal. Tissues with long T1 relaxation times (such as cysts, cerebrospinal fluid and edema) show as dark signal. In T2-weighted images, tissues that have long T2 relaxation times (such as fluids) appear bright.
In cerebral tissue, differences in T1 relaxation times between white and grey matter permit the differentiation of these tissues on heavily T1-weighted images. Proton density-weighted images also allow distinction of white and grey matter, with tissue signal intensities mirroring those obtained on T2-weighted images. In general, T1-weighted images provide excellent anatomic detail, while T2-weighted images are often superior for detecting pathology.
Gradient Recalled Echo Pulse Sequences
Gradient recalled echo (GRE) sequences, which are significantly faster than SE sequences, differ from SE sequences in that there is no 180 degree refocusing RF pulse. In addition, the single RF pulse in a GRE sequence is usually switched on for less time than the 90 degree pulse used in SE sequences. The scan time can be reduced by using a shorter TR, but this is at the expense of the signal to noise ratio (SNR) which drops due to magnetic susceptibility between tissues. At the interface of bone and tissue or air and tissue, there is an apparent loss of signal that is heightened as TE is increased. Therefore it is usually inappropriate to acquire T2-weighted images with the use of GRE sequences. Nevertheless, GRE sequences are widely used for obtaining T1-weighted images for a large number of slices or a volume of tissue in order to keep scanning times to a minimum. GRE sequences are often used to acquire T1-weighted 3D volume data that can be reformatted to display image sections in any plane. However, the reformatted data will not have the same in-plane resolution as the original images unless the voxel dimensions are the same in all three dimensions.
Paramagnetic Contrast Agents
MRI contrast agents are primarily paramagnetic agents designed to enhance the T1 and T2 relaxation times of adjacent hydrogen nuclei. Some agents are classified as T1 active or T2 active. They produce complex effects that vary depending on the RF pulsing sequence. For example, T1 shortening increases the RF signal intensity but T2 shortening decreases it. In many instances paramagnetic contras agents permit the visualization of lesion with shorter TR, thus decreasing scan time.
Paramagnetic contrast agents have been developed for oral, intravenous, and inhalation administration, and although this is an active research area in MRI, at the present time the IV agents have predominated. Gadolinium+3 (Gd+3), which has seven unpaired electrons, has the strongest relaxation rate properties and has proven effective in demonstrating various types of lesions. However, it is extremely toxic and is administered in a complex with DTPA (diethylenetriaminepentaacetic acid) (Gd-DTPA) to ensure detoxifification.
MRI Artefact
The term artefact refers to the occurrence of undesired image distortions, which can lead to misinterpretation of MRI data. The theoretical limit of the precision of measurements obtained from medical images is determined by the point spread function of the imaging device (Rossmann (1969) and Robson et al. (1997)). However, in practice, the limit is determined by the physiological movements of a living subject (e.g. respiration, heartbeat, twitching or tremor). The finite thickness of the slice of tissue imaged may also represent a constraint. If the signals arising from different tissue compartments cannot be separated within each voxel, then an artefact known as partial voluming is produced. This uncertainty in the exact contents of any voxel is an inherent property of the discretised image and would even exist if the contrast between tissues were infinite. Furthermore, chemical shift and susceptibility artefacts (Schenck (1996)), magnetic field and radio frequency non-uniformity, and Field of View and slice thickness calibration inaccuracies can all compromise the accuracy with which quantitative information can be obtained for a structure of interest in the living human body. A detailed analysis of all these effects is, however, beyond the scope of this article.
Gibbs Ringing or Truncation Artefact
This arises due to the finitie nature of sampling. According to Fourier theory, any repetitive waveform can be decomposed into an infinite sum of sinusoids with a particualr amplitude, phase and frequency. In practice, a waveform (e.g. MRI signal) can only be sampled or detected over a given time period and therefore the signal will be under-represented. The artefact is prominent at the interface between high and low signal boundaries and results in a 'ringing' or a number of discrete lines adjacent to the high signal edge.
Phase-wrap or 'Aliasing'
Aliasing can occur in either the phase or frequency direction but is mainly a concern in the phase direction. It is a consequence of Nyquist theory: the sampling rate has to be at least twice that of the highest frequency expected. The effect occurs whenever there is an object or patient anatomy outside the selected field-of-view but within the sensitive volume of the coil. In the frequency direction, this is avoided by increasing the sampling and use of high pass filters. By swapping the direction of phase/frequency encoding or using larger or rectangular fields-of-view the effect can be avoided.
Motion Artefacts (Ghosting)
Ghosting describes discrete or diffuse signal throughout both the object and the background. It can occur due to instabilites within the system (e.g. the gradients) but a common cause is patient motion. When movement occurs the effect is mainly seen in the phase direction. This is because of the discrepancy between the time taken to encode the image in each direction. Frequency encoding, done in one go at the time of echo collection, takes a few ms whereas phase encoding requires hundreds of repetitions of the sequence, taking minutes. Motion causes anatomy to appear in a different part of the scanner such that the phase differences are no longer consistent. Periodic motion e.g. respiratory or cardiac motion can be 'gated' to the acquisiton so that the phase encoding is performed at the 'same' part of the cycle. This extends imaging time as the scanner 'waits' for the appropriate signal but is effective in combating these artefacts. Modern scanners are now so fast that 'breathold' scans are replacing respiratoy compensation. Non-periodic motion e.g. coughing, cannot easily be remedied and patient co-operation remains the best method of reducing these artefacts. In this simple experiment a test object is moved gently during the scan. The effect is dramatic and due to the fourier transform nature of MRI, even this small displacment has produced artefacts throughout the image (the image is shown twice with different 'window' settings to enable the full extent of the artefact to be seen).
Chemical Shift
This artefact arises due to the inherent differences in the resonant frequency of the two main components of an MR image: fat and water. It is only seen in the frequency direction. At 1.5 Tesla there is approximately 220 Hz difference in the fat-water resonance frequency. If this frequency range has not been accommodated in the frequency encoding (governed by the receiver bandwidth and matrix size) then adjacent fat and water in the object will artificially appear in separate pixels in the final image. This leads to a characterisitic artefact of a high signal band (where the signal has 'built up') and an opposite dark band (signal void).
Susceptibility
The susceptibility of a material is the tendancy for it to become magnetised when placed in a magnetic field. Materials with large differences in susceptibility create local disturbances in the magnetic field resulting in non-linear changes of resonant frequency, which in turn creates image distortion and signal changes. The problem is severe in the case of ferromagnetic materials but can also occur at air-tissue boundaries. This example was acquired in a patient who had permanent dental work. It did not create any problems for the patient but the huge differences in susceptibility caused major distortions and signal void in the final image.
• Other Artefacts
An RF or zipper artefact is caused by a breakdown in the integrety of the RF-shielding in the scan room. Interference from an RF source causes a line or band in the image, the position and width of which is determined by the frequencies in the source. A Criss-cross or Herringbone artefact occurs when there is an error in data reconstruction.

Hardware
An MR system consists of the following components: 1) a large magnet to generate the magnetic field, 2) shim coils to make the magnetic field as homogeneous as possible, 3) a radiofrequency (RF) coil to transmit a radio signal into the body part being imaged, 4) a receiver coil to detect the returning radio signals, 5) gradient coils to provide spatial localization of the signals, and 6) a computer to reconstruct the radio signals into the final image. Each component contributes for making the examination faster and easier.
Magnet
Thera are different types of magnet used for diagnostic and research imaging. Permanent magnet has a field strength limited to 0.064 Tesla – 0.3 Tesla. While resistive magnet is ranging from 0.1 – 0.4 Tesla. Super conductive magnet almost unlimited. It can be low as 0.15 T and can go up to 7 T or higher. Cryogens and refrigeration are required for superconductive magnet to keep the system cool to maintain its strength. The stronger the magnet the higher the signal to noise ratio (SNR). Higher gradient system which is measured as mT/m per axes helps to decreased repetition time (TR) and echo imaging time. Shorter TRs and TEs normally reduced the scanning time down to subsecond imaging. With gradient development it is now possible to pursue real time MR scanning.
Radio Frequency (RF) coils
The body part to be examined determines the shape of the antenna coil to be used for imaging. Most coils are round or oval-shaped. And the body part to be examined is inserted into the coil’s open center. Some coils, rather than encircling the body part, are placed directly on the patien over the area of interest. These “ surface coils” are best for thin body parts, such as the limbs, or superficial portions of a larger body structure, such as the orbit within the head or the spine within the torso. Another form of surface coils is the endocavitary coil, in which the imaging coils is designed to fit within a body cavity, such as rectum. This enables a surface coil to be placed close to some internal organs which may be distant from surface coils applied to the exterior body. Endocavitary coils also may be used to image the wall of the cavity itself.
Gradients
The principle role of the gradient coils are to produce linear chnages in magnetic field in each of the x,y and z directions. By combining gradients in pairs of directions, oblique imaging can be performed. Gradient specifications are stated in terms of a slew rate which is equal to the maximum achievable amplitude divided by the rise time. Typical modern slew rates are 150 T/m-s. The gradient coils areshielded in a similar manner to the main windings. This is to reduce eddy currents induced in the the cryogen which would degrade image quality.
Safety of MRI
MRI is generally considered safe. Since MRI does not use ionizing radiation. Nevertheless, a number potential safety issues concerning MRI must be raised, some related to potential direct effects on the patient from the imaging environment and others related to indirect hazards
Static Field Effects
The most obvious safety implication is the strength of the magnetic field produced by the scanner. There are three forces associated with exposure to this field: a translational force acting on ferromagnetic objects which are brought close to the scanner (projectile effect), the torque on patient devices/implants, and forces on moving charges within the body, most often observed as a superposition of ECG signal. In the main, sensible safety precautions and the screening of patients means that there are seldom any problems. Of major concern is the re-assessment of medical imaplants and devices deemed safe at 1.5 Tesla which may not have been tested at higher fields. This is becoming an issue as 3.0 T scanners become more commonplace.
The extension of the magnetic field beyond the scanner is called the fringe field. All modern scanners incorporate additional coil windings which restrict the field outside of the imaging volume. It is mandatory to restrict public access within the 5 Gauss line, the strength at which the magnetic field interfers with pacemakers.
Gradient Effects
These come under the term 'dB/dt' effects referring to the rate of change in field strength due to gradient switching. The faster the gradients can be turned on and off, the quicker the MR image can be acquired. At 60 T/s peripheral nerve stimulation can occurr, which although harmless may be painful. Cardiac stimulation ocurrs well above this threshold. Manufacturers now employ other methods of increasing imaging speed (so called 'parrallel imaging') in which some gradient encoding is replaced.
RF Heating Effects
The repetitive use of RF pulses deposits energy which in turn causes heating in the patient. This is expressed in terms of SAR (specific absorption rate in W/kg) and is monitored by the scanner computer. For fields up to 3.0 Tesla, the value of SAR is proportional to the square of the field but at high fields the body becomes increasingly conductive neccessitating the use increased RF power. Minor patient burns have resulted from use of high SAR scans plus some other contributory effect, e.g. adverse patient or coil-lead positioning, but this is still a rare event.
Noise
The scans themselves can be quite noisey. The Lorentz forces acting on the gradient coils due to current passing through them in the presence of the main field causes them to vibrate. These mechanical vibrations are transmitted through to the patient as acoustic noise. As a consequence patients must wear earplugs or head phones while being scanned. Again, this effect (actually the force on the gradients) increases at higher field and manufactures are using techniques to combat this including lining the scanner bore or attaching the gradient coils to the scan room floor thereby limiting the degree of vibration.

Claustrophobia
Depending on the mode of entry into the scanner (e.g. head first or feet first) various sites have reported that between 1 % and 10 % of patients experience some degree of claustrophobia which in the extreme cases results in their refusal to proceed with the scan. Fortunately, modern technology means that scanners are becoming wider and shorter drastically reducing this problem for the patient. In addition, bore lighting, ventilation as well as the playing of music all help to reduce this problem to a minimum.
Bioeffects
There are no known or expected harmful effects on humans using field strengths up to 10 Tesla. At 4 Tesla some unpleasant effects have been anedoctally reported including vertigo, flashing lights in the eyes and a metallic taste in the mouth. Currently pregnant women are normally excluded from MRI scans during the first trimester although there is no direct evidence to support this restriction. The most invasive MR scans involve the injection of contrast agents (e.g. Gd-DTPA). This is a colourless liquid that is administered i.v. and has an excellent safety record. Minor reactions like warm sensation at the site of injection or back pain are infrequent and more extreme reactions are very rare.

Summary
MRI uses magnetism and radio frequencies (RF) to create diagnostic sectional images of the body. If the nucleus is spinning, it has angular momentum, or nuclear magnetic moment. This rotating charge acts as a current loop and produces a magnetic field. When a rotating nucleus is subjected to a magnetic field, it will begin to precess. MR imaging is accomplished through various measurements of this movement of the nuclear magnetic field.
The frequency of procession is called the larmor frequency and is critical to MR imaging. Production of the nuclear magnetic resonace signal requires applying a larmor frequency alternating RF and then listening to the RF emissions from the proton. Digital Imaging reconstruction techniques are then used to create sectional and three-dimensional images.
The primary parameters used to modify and control the MRI process include proton spin density, repetition time (TR), echo time (TE), inversion time (TI), T1 and T2. The parameter that are used vary depending on the pulse sequence used. The RF signal strength determines brightness, although it is also affected by field strength, section thickness, the MRI parameter, motion, spatial resolution, S/N, and scan time.

Read More..

THE BASIC PRINCIPLES OF COMPUTED RADIOGRAPHY

THE BASIC PRINCIPLES OF COMPUTED RADIOGRAPHY
By : Sumarsono


Computed radiography (also known as diagnostic digital radiography), often abbreviated CR, refers to conventional projection radiography, in which the image is acquired in digital format using an imaging plate rather than film. Computed radiography (CR) system was introducing the image plate (IP), a product of the latest technology which has made a great, in detecting and recording X-ray images information of high quality and sensitifity. CR image can also be viewed on workstation. The images will be quickly transmitted through electrical lines and display on Cathode Ray Tube (CRT). Image processing using CRT will assist radiologist in making high quality diagnosis. Furthermore, storing images on optical disk will facilitate efficient archieving, even when space is limited.



The Computed Radiography System

Computed radiography is performed by a system consisting of the following functional components:
• A digital image receptor (The Imaging Plate)
• A digital image processing unit
• An image management system
• Image and data storage devices
• Interface to a patient information system
• A communications network
• A display device with viewer operated controls
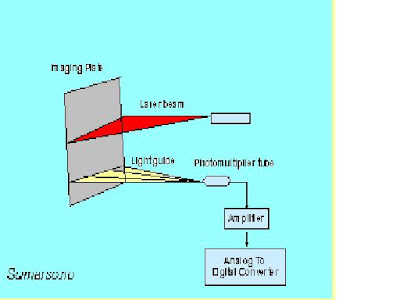
In place of the traditional screen and film, computed radiography use the imaging plate as a digital image receptor. Although the imaging plate looks very similar to traditional screen, it function much differently. The digital receptor is the device that intercepts the X-ray beam in photo stimulable phosphor after X-ray beam has passed through the patients body and produces an image in digital form, that is, a matrix of pixels, each with a numerical value and allowing this images information of electrical signal. The receptor is in the form of a matrix of many individual pixel elements. They are based on a combination of several different technologies, but all have this common characteristic: when the pixel area is exposed by the x-ray beam (after passing through the patient's body), the x-ray photons are absorbed and the energy produces an electrical signal. This signal is a form of analog data (latent image) that is then converted into a digital number and stored as one pixel in the image.

The image plate reader is another important component of the image acquisition control in computed radiography. The image reader converts the continuous analog information (latent image) on the imaging plate to a digital format. • In this unit the screen is scanned by a very small laser beam. When the laser beam strikes a spot on the screen it causes light to be produced (the stimulation process). The light that is produced is proportional to the x-ray exposure to that specific spot.

The result is that an image in the form of light is produced on the surface of the stimualible phosphor screen. A light detector measures the light and sends the data on to produce a digitized image. As the surface of the stimualible phosphor screen is scanned by the laser beam, the analog data representing the brightness of the light at each point is converted into digital values for each pixel and stored in the computer memory as a digital image.

Radiographic Condition
Computed radiography can be carried out under the same condition for general radiography by only replacing a conventional film / screen system with an imaging plate, dose and quality of X-ray, among the parameter given to images, are qualively different from those for screen-film system.

Gradian processing is done via computer operation to optimize image contras and optical density. Image contrast can be adjusted as desired, in accordance with the anatomical region and diagnostic purpose. The shape of gradian curve can also be changed, dark and white reversal can be easily archieved. Spatial Frequency is used for enhancing both the edges of anatomical region and structure of a certain size, and the basic contras curve is used as base from which contrast and density can be adjusted as fairly as desired. Image processing improves diagnostic accuracy and expand diagnostic scope.

Two types of image processing are involved : 1). Gradation Processing ; Incline of the gradation curve, shape of the gradation curve, density which determines incline of gradation curve, and degree of parallel movement of gradation curve. 2). Spatial Frequency Response Processing ; Frequency to emphasize in frequency processing, shape of emphasize curve depending on density frequency processing, Degree of emphasis in frequency processing.
Gradation Processing and Spatial Frequency Response Processing are use to control the contrast and density of the displayed image. Gradation Processing controls the range of densities use to display structures on the image ; Gradation Processing is similar to window setting used in CT-Scan. Spatial Frequency Response Processing controls the sharpness of boundaries betwen two structures of different density.


The wide dynamic range and linear response of the typical digital receptor is like a "two-edged sword". The advantage is that a wide range of exposures, and exposure errors, will still produce good image contrast. That is, the loss of contrast with exposure error is not a limiting factor as it is with film. Even though images with good contrast can be produced with relatively low exposures, they will have a high level of quantum noise. We recall from other modules that the level of image (quantum) noise depends on the exposure to the receptor. When a low exposure is used, the result can be excessive image noise. The other problem is that excessively high and unnecessary exposures can be used to form images. While these images will have good quality (low noise) there will be unnecessary exposure to the patient. This problem does not exist with film radiography because the increased exposure will result in a visibly overexposed film.
In general, for a radiographic procedure there is an optimum exposure that produces a good balance between image noise and patient exposure. The challenge to the technologist is to make sure that the technique factors are set to produce this optimum exposure.
Quality Characteristics
Computed radiography have the five specific quality characteristics : contrast, detail, spatial, artifacts and noise. The contrast sensitivity of a computed radiographic procedure and the image contrast depend on several factors. Two of these, the x-ray beam spectrum and the effects of scattered radiation are similar to film radiography. Computed radiography is the ability to adjust and optimize the contrast after the image has been recorded. This usually occurs through the digital processing of the image and then the adjustment of the window when the image is being viewed.
Detail is reduced and limited by the blurring that occurs at different stages of the imaging process both computed and film radiography are three sources of blurring:
• The focal spot (depends on size and object location)
• Motion (if it is present)
• The receptor (generally because of light spreading within the fluorescent or phosphor screen)
Computed radiography is that additional blurring is introduced by dividing the image into pixels. Each pixel is actually a blur. The size of a pixel (amount of blurring) is the ratio of the field of view (image size relative to the anatomy) and the matrix size. Pixel size is a factor that must be considered because it limits detail in the images.
The most predominant source of noise in digital radiography is generally the quantum noise associated with the random distribution of the x-ray photons received by the image receptor. The level of noise depends on the amount of receptor exposure used to produce an image. With computed radiography it can be adjusted over a rather wide range because of the wide dynamic range of the typical digital receptor. The noise is controlled by using the appropriate exposure factors.
Three factors are directly responsible for computed radiography image resolution : 1). The dimension of the crystals in the imaging plate, 2). The size of the laser beam in the reader, and 3). The image-reading matrix. Computed radiography contrast resolution is currently greater than that of conventional film, but spatial resolution is slightly less than that film.
Benefits of Computed Radiography
When using a computed radiography system certain benefits are readily apparent, including the following :
Improved Diagnostic Accuracy and Expanded Diagnostic Scope ; By storing laser-scanned x-ray images on high-sensitivity imaging plates, minute differences in x-ray absorbtion, are detected, providing highly detailed and easily readable diagnostic information. The wide exposure latitude permits diagnosis on an entire area of interest, allowing imaging from bones to soft tissue with a single exposure. Computer analysis of images can provide increased diagnostic information to assist in the medical treatment of a patient.
X-ray Dosage Reduction ; The high-speed imaging plate coupled with the efficient information read-out of the high-precision laser spot scanning device allows the patient to be exposed to a lower x-ray dose than that using a conventional film-screen system. This is especially worthwhile for pediatric examinations. Reductions vary somewhat with the type of examination performed, as shown in table below :

Comparison of radiographic film H and D response curve
To linear imaging plate response


Repeat Rate Reduction ; Because of the computed radiography system’s wide technique latitude, technical errors are easily corrected to provide prime diagnostic information. When a film-screen combination is used, technical errors in either direction can markedly degrade the image quality. Technical errors have much less effect on the final quality of a computed radiographic image. This benefit obviously increases throughput and reduces the patient’s discomfort, because it lessens the need to repeat the examination. The technical latitude of computed radiography is a tremendous asset in the area of portable radiography.
Teleradiographic Transmission ; Image Plate reader devices can be linked via dedicated phone lines, microwave transmission or other teleradiographic means to centralize the review of image data. This means of image sharing could obviously benefit affiliated hospitals or clinic that are separated by large geographic distances and share professional staff. Teleradiology could also provide immediate consultation with specialists, which benefits not only the patient but also the level of efficiency of the institution.
Department Efficiency ; The computed radiography system eliminates all darkroom work. With this factor plus the previous benefits, departemental efficiency is ultimately increased.
Summary
Computed Radiography uses image receptors with barium fluorohalide screens that function quite differently from intensifying screens in that a latent image is stored upon exposure to ionizing radiation. The latent image can be released upon stimulation by light. The incident photon beam produces a latent image within the fluorohalides. The flourohalides are stimulated by a laser, which causes them to emit light. The light beam is then detected by a photomultiplier tube which digitizes the image. Display and storage then proceed as with any other digital image. Although resolution continues to be a problem, pasien dose is dramatically reduced, and digital contrast and latitude control are superior.

Read More..